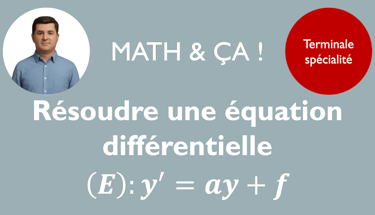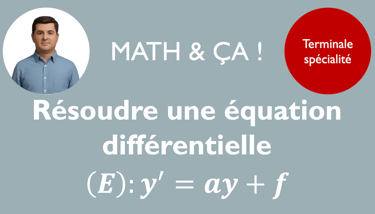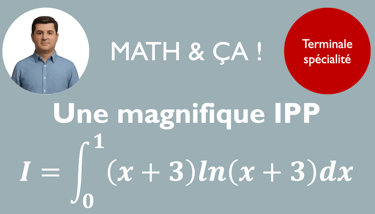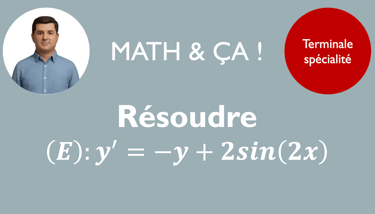Primitives de fonctions usuelles et équations différentielles

La notion de primitive est intuitivement très facile à comprendre. Déterminer une primitive d'une fonction, c'est le contraire de dériver une fonction. Ceci étant posé, comment faire pour déterminer une primitive? Quelle technique mettre en oeuvre?

Tout d'abord, il y une différence entre déterminer une primitive, la primitive ou les primitives. Ensuite, la notion de fonction composée va très sérieusement compliquer l'histoire. Enfin la notion de primitive est associée à celle d'équation différentielle.

Il s'agit d'une équation mettant en jeu une fonction et sa dérivée (premier ordre en Terminale Spécialité), dont l'inconnue est donc une fonction. La résolution d'équations différentielles est très importante car elle est utilisée en physique notamment. C'est donc un chapitre technique et fondamental pour l'année de Terminale spécialité.

Il sera suivi par le chapitre sur les intégrales qui reprendra toutes les techniques apprises ici.

Enfin, on apprendra la technique de l'intégration par parties qui permettra, dans certains cas, de déterminer les primitives de fonctions écrites sous la forme d'un produit.

Les Documents en Ligne

Liste des vidéos du chapitre