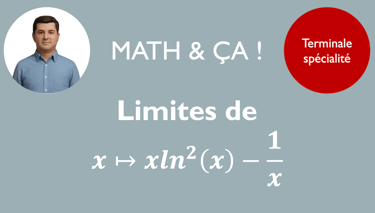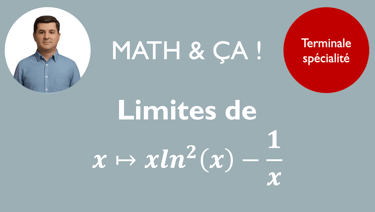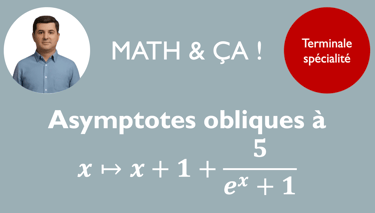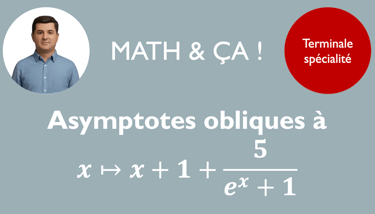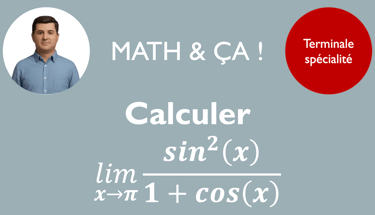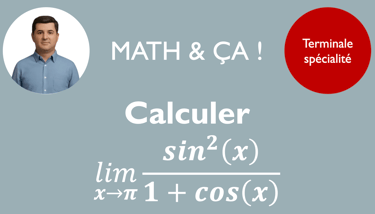Limites de fonctions

Après avoir travaillé les limites de suites en début d'année, on s'intéresse ici à la notion de limites de fonctions. On passe finalement du cas discret au cas continue.

On reprend de nombreuses compétences du chapitre précédent pour calculer la limite d'une fonction au voisinage de l'infini. On va également évaluer la limite d'une fonction au voisinage d'un nombre. C'est finalement la connaissance du domaine de définition qui va vous indiquer à quel endroit chercher.

Ces calculs de limites  vont induire la recherche d'asymptote à une courbe. Elle peut être horizontale, verticale ou même oblique. La recherche d'une asymptote oblique à une courbe est à la limite du programme mais est très accessible. Vous avez ci-dessous une fiche méthode pour cette notion.

La détermination des limites d'une fonction permettra in fine de compléter le tableau de variation qui devient un vrai résumé de la fonction sur son domaine de définition.

Les Documents en Ligne

Liste des vidéos du chapitre